Dynamic System Inspired Adaptive Time Stepping Controller for Residual Networks Families

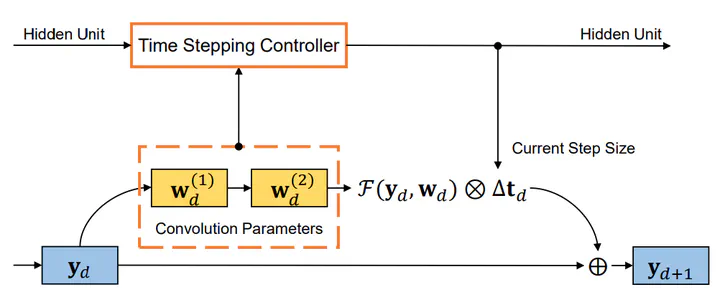
The correspondence between residual networks and dynamical systems motivates researchers to unravel the physics of ResNets with well-developed tools in numeral methods of ODE systems. The Runge-Kutta-Fehlberg method is an adaptive time stepping that renders a good trade-off between the stability and efficiency. Can we also have an adaptive time stepping for ResNets to ensure both stability and performance? In this study, we analyze the effects of time stepping on the Euler method and ResNets. We establish a stability condition for ResNets with step sizes and weight parameters, and point out the effects of step sizes on the stability and performance. Inspired by our analyses, we develop an adaptive time stepping controller that is dependent on the parameters of the current step, and aware of previous steps. The controller is jointly optimized with the network training so that variable step sizes and evolution time can be adaptively adjusted. We conduct experiments on ImageNet and CIFAR to demonstrate the effectiveness. It is shown that our proposed method is able to improve both stability and accuracy without introducing additional overhead in inference phase.

Conference paper

AAAI Conference on Artificial Intelligence